Генерация всевозможных комбинаций из набора символов — комбинаторика в Python (itertools)

Статьи / Python

Встроенный модуль itertools в Python — простой инструментарий, позволяющий генерировать полный список возможных комбинаций из заданного набора символов. Как с этим работать и справляться - далее в статье.

Что ж, в преддверии Нового года KOTOFF.net вновь расправляет крылья.

И сразу к делу. Рассмотрим всего 3 функции и их различия. 

1. Нахождение всевозможных комбинаций из набора символов

Допустим, у нас есть некий алфавит из трёх букв (А, Б, В), и из него необходимо составить максимальное количество трёхзначных слов (комбинаций). Причём в данном случае буквы могут повторяться. Алфавит короткий, однако у нас получится составить целых 27 слов. На каждую позицию приходится по 3 варианта букв, соответственно, общее количество комбинаций можно посчитать так: n^k (n - количество доступных символов в степени k - длина конечной комбинации). Для нашего случая: 3³ = 27

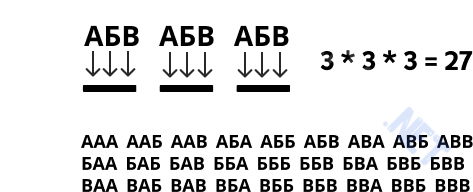
Теперь импортирую itertools и сгенерирую всё то, что выше считали руками, но теперь уже с помощью функции product():

from itertools import product


for i in product('АБВ', repeat=3):
    print(''.join(i), end=' ')

Функция принимает два параметра (набор символов и длина конечного объекта). С помощью join() получили строковое представление полученной комбинации.

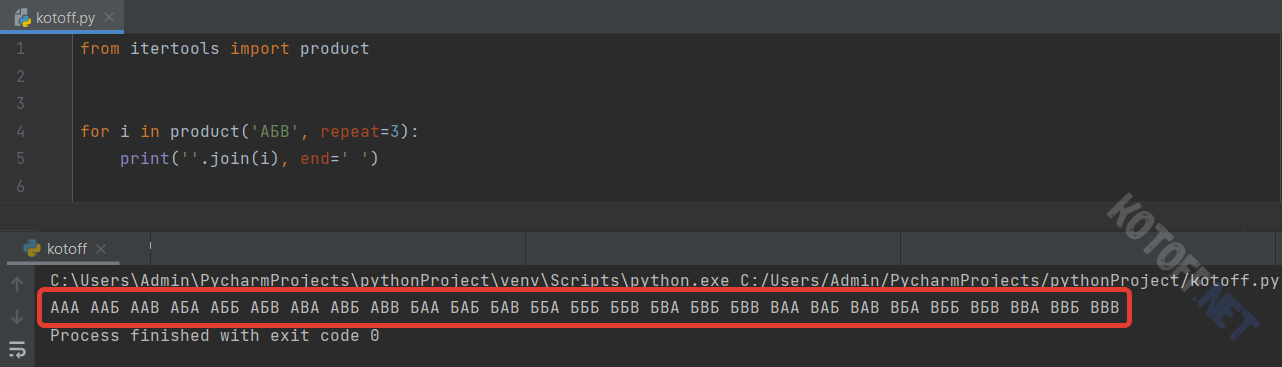И, как можно заметить, в результате мы получили те самые 27 так называемых слов.

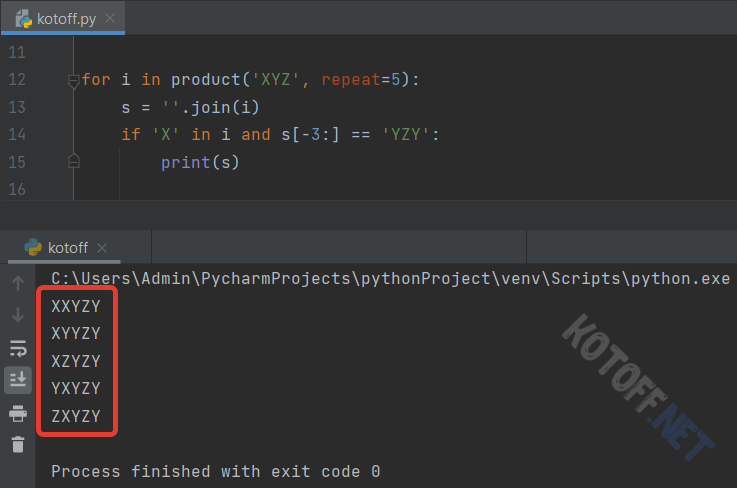
Можно добавить в цикл некий фильтр (условие). Например, сделаю так, чтобы комбинируемые слова начинались только с "X" и заканчивались на "YZY":

Попробуем сгенерировать всевозможные автомобильные номера для одного региона. Способ, конечно, не особо рациональный, но для примера сгодится:

from itertools import product
import re


chars = '0123456789АВЕКМНОРСТУХ'
reg = '[АВЕКМНОРСТУХ]{1}\d{3}[АВЕКМНОРСТУХ]{2}'

for i in product(chars, repeat=6):
    if re.fullmatch(reg, ''.join(i)):
        print(''.join(i))

Кстати, если добавить в цикл счётчик, то в итоге получим цифру 1.728.000 (12*10*10*10*12*12). Именно столько номеров формата x000xx можно наклепать для одного региона :)

2. Перестановка символов в наборе

В отличие от предыдущего примера, теперь мы не можем использовать по несколько раз один и тот же символ. Можем только переставлять их местами. Принцип подсчёта количества комбинаций остаётся тот же: необходимо перемножить количество вариантов символов на каждую позицию слова между собой. Но поскольку по мере составления слова на каждую последующую позицию символов будет оставаться всё меньше и меньше, то и формула также меняется на: n! / (n-k)! (n - количество доступных символов, k - длина слова). Если n = k, то можно использовать упрощённую формулу: n! (факториал числа n).

В питоне для таких целей используется функция permutations(). Принимает тоже два параметра: набор символов и длину генерируемой комбинации:

from itertools import permutations

for i in permutations('АБВ'):
    print(''.join(i))

Из трёх букв будет сгенерировано 6 различных слов с неповторяющимися символами (1! = 1 * 2 * 3 = 6)

Попробуем составить трёхзначные слова в 5-символьном алфавите (5! / (5-3)! = 120 / 2 = 60):

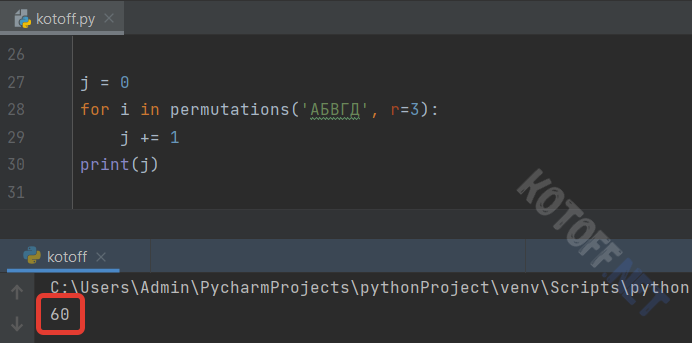
Кстати, если в заданном "алфавите" есть повторяющиеся символы, то они будут повторяться и в комбинациях:

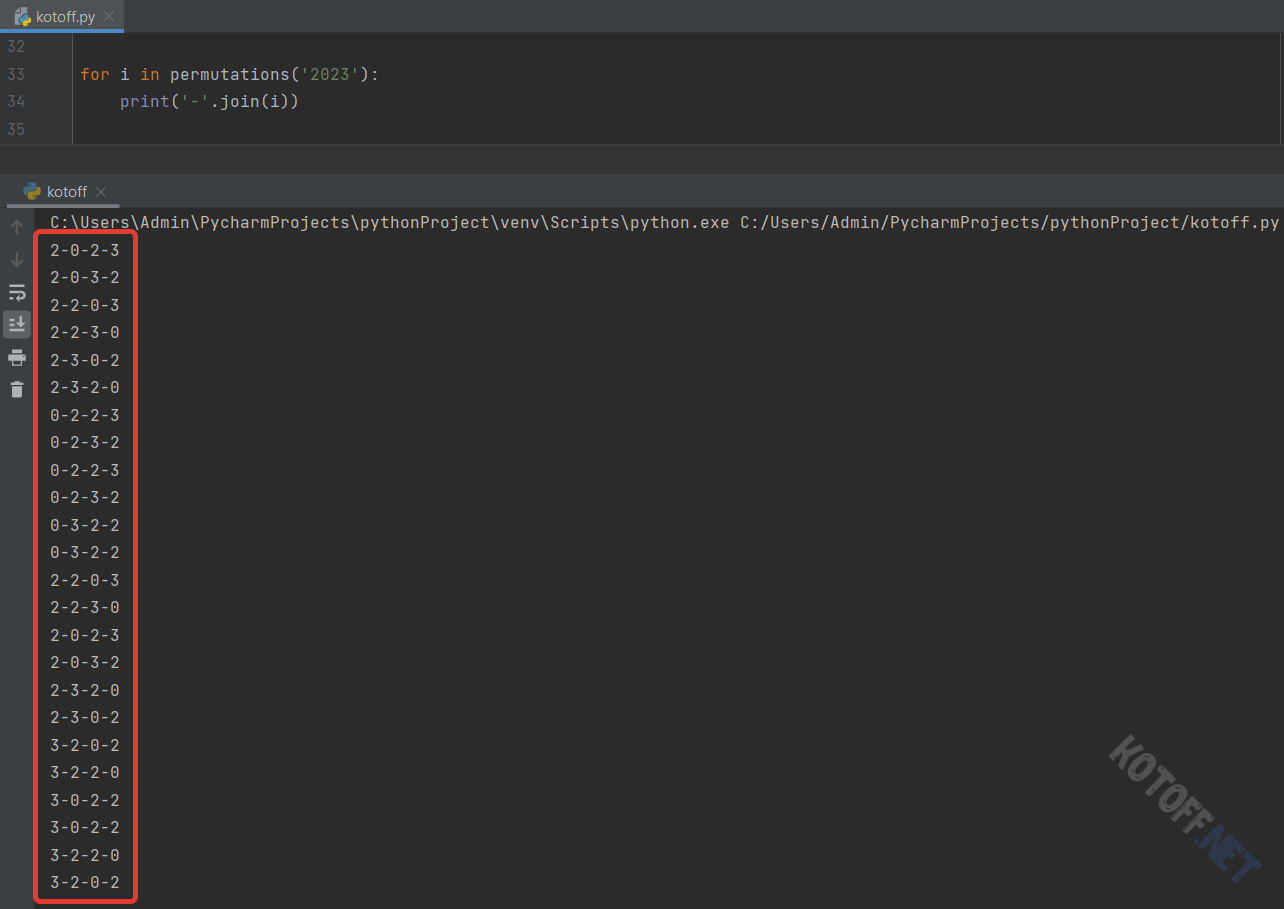
3. Сочетания без повторений

А если нужно составить не комбинации, а отдельные неповторяющиеся сочетания? Например, есть 6 человек. Вопрос: какими способами их можно разбить по парам? Опять же, пользуемся формулой: n! / (n-k)! / k! (n - количество доступных объектов/символов, k - количество сочетаний). Соответственно, существует 6! / (6-2)! / 2! = 720 / 24 / 2 = 15 вариантов разбиения этих 6 персон по парам.

Теперь реализуем эту задачу на питоне с помощью функции combinations(). Принимает она два параметра - список и кол-во сочетаний:

from itertools import combinations

for i in combinations(['Юля', 'Даша', 'Соня', 'Дима', 'Игорь', 'Вадим'], 2):
    print(' - '.join(i))

Результат работы программы будет таков:

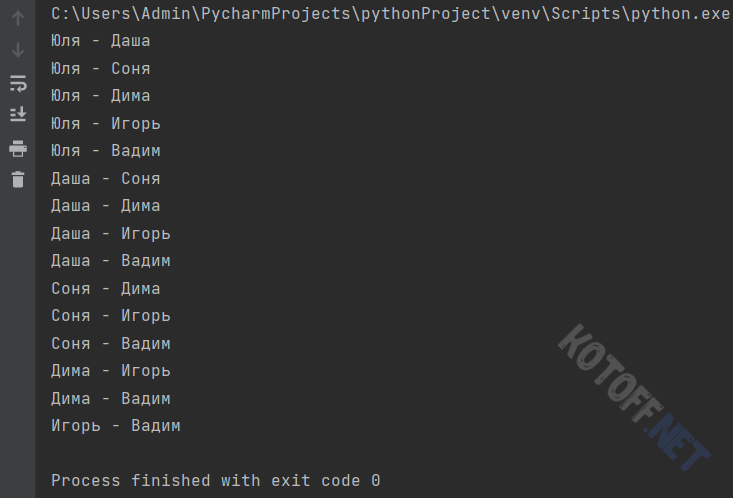
На этом, пожалуй, на сегодня всё. С наступающим!